Contenido
0. Definiciones
Promedio: Suma de los números dados divididos por la cantidad de datos. Ejemplo: 8 + 5 + 17 = 30, ahora divida 30 entre 3 para obtener un promedio de 10.
1. Teoría
Grados
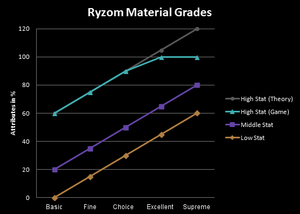
Hay 5 grados de materiales en Ryzom y cada grado tiene un valor promedio asignado. Si usted busca cualquier material de un grado dado y calcula el valor promedio de sus estadísticas, usted finalizará con la siguiente lista:* 20 para Básicos
- 35 para Finos
- 50 para Selectos
- 65 para Excelentes
- 80 para Supremos
Estos valores también determinan el prefijo de un ítem fabricado. Sí usted calcula el valor promedio de las estadísticas de un ítem fabricado mostrado en la vista previa y lo compara con el cuadro dado arriba, usted puede determinar el prefijo de ítem. Sí su valor promedio está sobre el promedio del grado, el prefijo será aquel de grado inmediatamente superior. Por ejemplo, si su promedio está entre 51 y 65, el prefijo será excelente. Sí es 50 será Selecto. Parece trabajar en muchos casos, pero han ocurrido algunas excepciones a esta regla debido al redondeo u otros aspectos.
Estadísticas de los Materiales
Todas las materias primas siguen cierta regla sobre como se estructuran sus estadísticas. Hay siempre un valor mayor que todos los demás y dos valores que son menores a todos los demás. Los valores remanentes están entre estos extremos y son iguales en número. Ellos representan el promedio del material y encajan con su grado. El mayor valor es 40 sobre el promedio y los dos valores menores son 20, debajo del promedio. Ellos se cancelan unos a otros de este modo +40 -20 -20 = 0. El material tiene un valor promedio perfecto y encaja con la tabla. Así, todo es Fino (¿O excelente?).
2. Realidad (En el juego)
Si tomamos la teoría explicada anteriormente y la aplicamos a un material Excelente, finalizaremos con un alto valor estadístico de 65 + 40 = 105. ¡Para un material Supremo es entonces 80 + 40 = 120! Sin embargo, todos los materiales están limitados a valores entre 0 y 100, así que estos son simplemente cortados en el juego... ¿Es éste un problema? Sí, desafortunadamente lo es. Si calculamos el promedio con estos nuevos valores los mayores y menores no se cancelan entre sí. El promedio del material es menor que lo supuesto y el material es degradado.
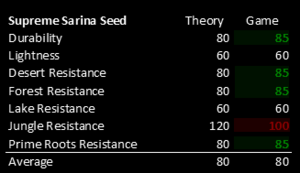
Ejemplo: Semillas Supremas (Engaste de la Joya)
Tiene 7 estadísticas: 1x alta a 100, 2x bajas a 60 y el resto de sus valores al grado promedio para supremo, el cual es 80. Ahora calculemos el promedio del material con el corte de los valores en mente. ¡(1x 100 + 2x 60 + 4x 80) dividido por 7 es 77.1! Pero debería ser 80 de acuerdo a la teoría. ¡El material es 3% peor que lo supuesto! Para corregir esto, los valores en el medio de la estadística han sido cambiados en el juego de 80 a 85. (1x 100 + 2x 60 + 4x 85) dividido por 7 es 80. ¡Listo!
Regla General: La cantidad de corrección necesaria en las estadísticas promedio depende del número total de estadísticas que el material tiene. Veamos ambos extremos en el siguiente párrafo. Chaqueta de municiones con 4 estadísticas y Foco Mágico con 11 estadísticas.
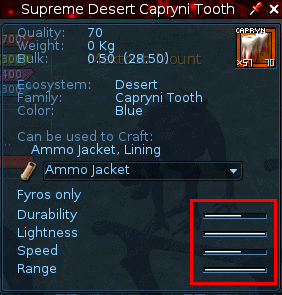
Ejemplo: Chaqueta de Municiones (Dientes Supremos de Capryni)
Solamente tiene 4 atributos. Si calculamos el promedio, finalizaremos con (1x 100 + 2x 60 + 1x 80) dividido por 4 es 75. ¡Uy! Para corregir esto, debemos añadir 20 a los estadísticos medios, ¡llevándolo de 80 a 100! Ahora luce de este modo: (1x 100 + 2x 60 + 1x 100) dividido por 4 es 80. ¡Perfecto! Ahora el material parece tener dos valores estadísticos altos, pero en realidad es solo un único valor alto y uno medio, el cual ha sido ajustado para corregir el promedio errado.
Ejemplo: Foco Mágico (Ámbar Supremo de Beng)
Tiene 11 atributos. Si calculamos el promedio, obtendremos: (1x 100 + 2x 60 + 8x 80) dividido por 11 es 78.2. ¡Cerca! Esto es lo más cerca que podemos estar del promedio ideal. Es necesaria una corrección menor de 80 a 82. (1x 100 + 2x 60 + 8x 82) dividido por 11 es 79.6. Sí fuera 83, estaría por encima de 80. El mismo principio aplica para materiales Excelentes, el rango de los estadísticos medios en este caso irá de 65 a 70. ¿Por qué esto es importante? Porque una vez que se usa un material Excelente y Supremo, los promedios ideales para los grados no encajan con el juego. Los promedios son un factor importante para los valores en la ventana de vista previa, así que es bueno mantenerlo en mente.
¡Gracias por leerme!
| Las Guías de Artesanía de Arcueid Artesanía y Colores ⚪ Artesanía y Materiales ⚪ Artesanía y Matemáticas |